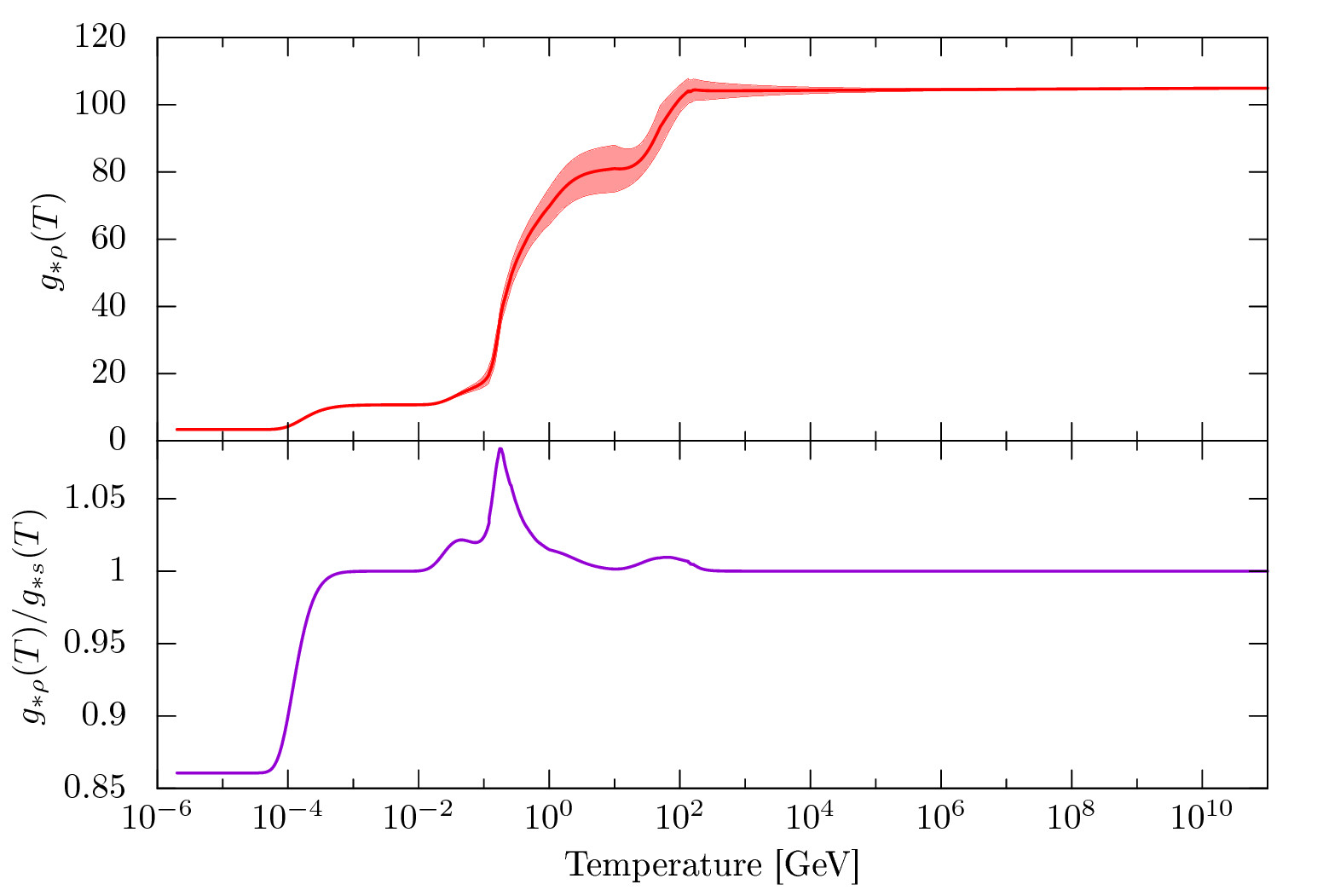
Effective degrees of freedom.
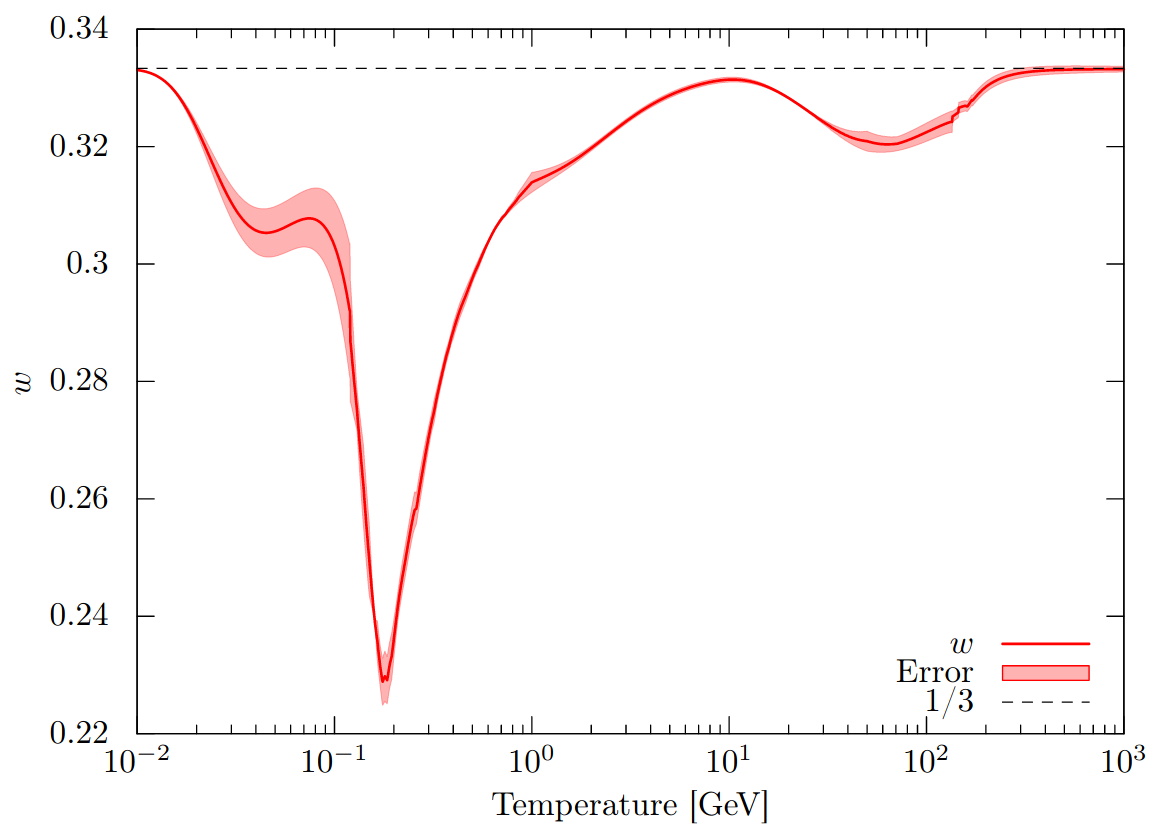
Equation of state.
Update: The equation of state parameter \( w \) data was newly added on 2024-07-19.
Tabulated data of the effective degrees of freedom and the transfer function estimated in this paper are distributed.
You can get the data for the effective degrees of freedom \( g_{*\rho,s} \) here and the equation of state parameter \( w \) here.
We also provide a C++ code for the fitting functions.
The data for the transfer function are available here.
If you find any problems or request additional data, please contact me (satoshi.shirai_at_ipmu.jp).

Effective degrees of freedom. |

Equation of state. |
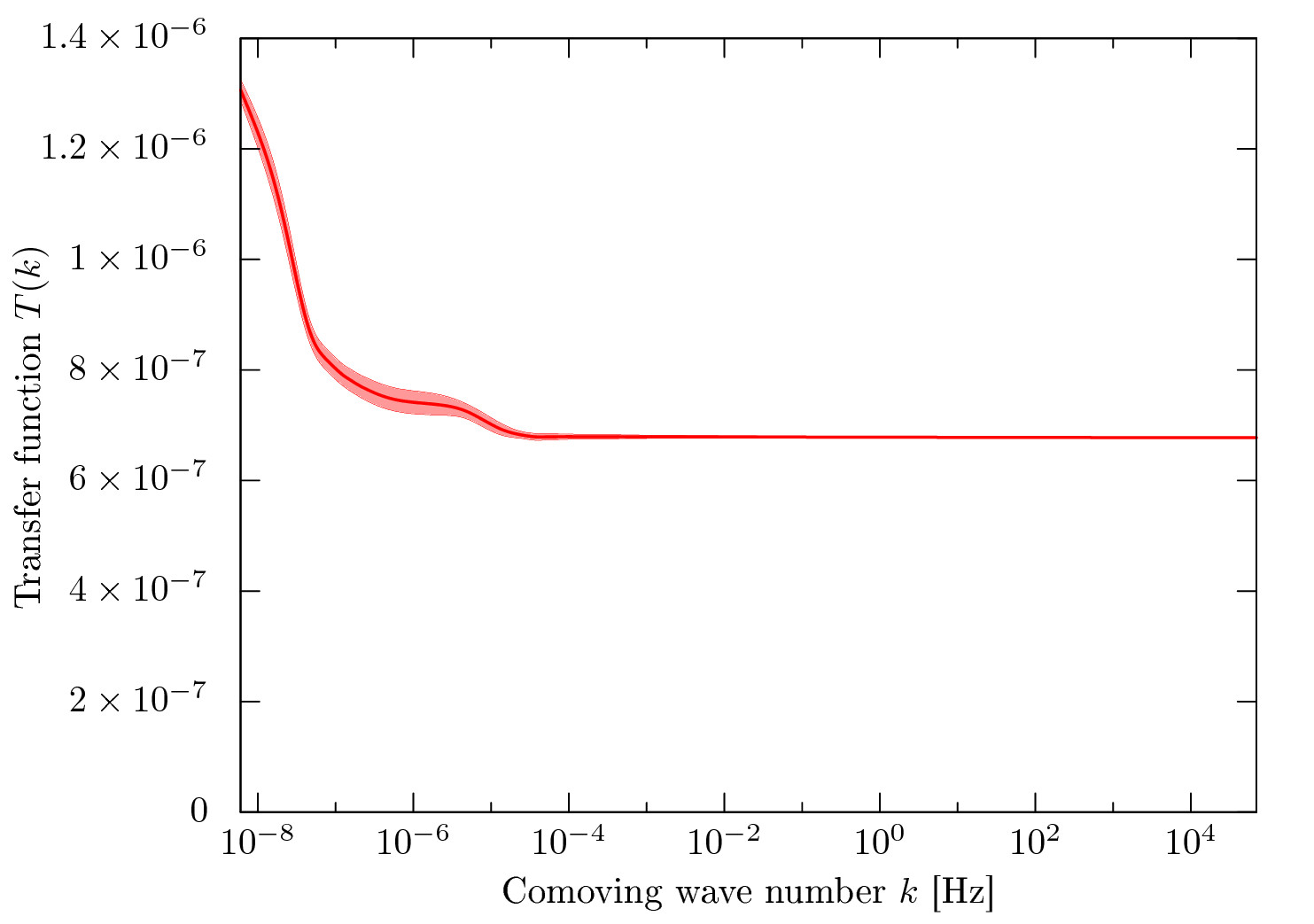
Transfer function. |