.
Based on the lectures given at Nagoya, Tohoku and Rikkyo University.
Available as arXiv:1312.2684v2.
You can buy a printed version from Springer or Hindustan Book Agency.
The errors below are relative to arXiv:1312.2684v2.
| place | content | thanks to |
| (3.3.2): | The RHS is missing $i/(2\pi)$. | T. Procházka |
| (4.3.6): | $dz/(xz)$ should be $dz/(2xz)$ | T. Procházka |
| (4.3.7): | $dz/(xz)$ should be $dz/(2xz)$ | T. Procházka |
| One line below (4.4.2): | The mass term should be $-\int d^2\theta m u$. | T. Procházka |
| Two lines below (5.2.5): | $\int_{P_0}^P dz/(xz)$ should be $\int_{P_0}^P dz/(2(xz-\Lambda))$. | T. Procházka |
| (5.3.1): | The discriminant of (5.2.11) is the cube of what was written in (5.3.1). | T. Procházka |
| (6.3.6): | The RHS should have $1/3!$ in front. | T. Procházka |
| (7.1.5): | The RHS should have $-1$ in front. | T. Procházka |
| Sec.7.3 | The mass parameters are all set to zero implicitly. | T. Procházka |
| One line below (7.3.7) | The last term should be $|\tilde Q_2|^2$. | T. Procházka |
| Sec.8.3 and Sec.8.4 | The singularities on the $u$-plane of the $N_f=2$ theory are at $u=0$ and $u=-4\Lambda^2$, not at $u=0$ and $u=-\Lambda^2$ as written in many places. | T. Procházka |
| (9.1.1): | $a_D=\tau_{UV} a$ should be $a_D=2\tau_{UV} a$ | Tom Burton |
| (9.1.3): | $a_D=\tau_{UV} a$ should be $a_D=2\tau_{UV} a$ | Tom Burton |
| One line below (9.1.7) | $1-z-f/z$ should be $1-\tilde z-f/\tilde z$. | T. Procházka |
| (9.2.16): | SU(3)$_D$ should be SU(2)$_D$. | S. Nawata |
| Two lines above (9.3.1) | A, B, G should be at $z'=\infty,$ $1$, $0$ instead. | T. Procházka |
| (9.4.12): | The numerator of the second term should be $\mu_1+\mu_2$. | T. Procházka |
| The paragraph below (10.1.1): | The A-cycle and the B-cycle are around $z=-1$, not around $z=0$. | T. Procházka |
| (10.1.6): | The RHS should have $+(\delta z)^3$ instead of $-(\delta z)^3$ | T. Procházka |
| (10.1.9): | The second equation should be $[\delta z]=2/5$ instead of $[\delta x]=2/5$ | T. Procházka |
| (10.3.4): | The numerator on the RHS should have $1,z,z^2,z^3,z^4$ instead of $1,z,z,z^2,z^3$. | T. Procházka |
| (11.1.6): | The RHS is missing $i$. | T. Procházka |
| A few lines below (11.2.8): | $y$ should be $\Lambda^N(z+1/z)$. | T. Procházka |
| Footnote 15 attached to (11.2.14): | The final $\chi(S)$ should be $\chi(\Sigma)$. | T. Procházka |
| (11.3.15): | The RHS should have $-1$ in front. | T. Procházka |
| (11.5.3): | $\tilde u_N$ should be $\delta u_N$. | T. Procházka |
| (11.5.10) and (11.5.11): | There are various minor mistakes in the computations in these equations and the explanations around it. The result (11.5.12) and the following discussions are OK. | T. Procházka |
| One line below (11.5.16): | $\delta zdz$ should be $\delta z dx$. | T. Procházka |
| One line below (12.1.1): | The theory with nonzero $\tilde\mu$ are not superconformal. | T. Procházka |
| (12.1.6) and (12.1.8): | $\mu'$ needs to be defined as $-(\sum \tilde\mu_i')/N$ with a minus sign in front. | T. Procházka |
| (12.1.10): | $u_k$ here is a certain dimensionless coefficient times $u_k$ in (12.1.9). | T. Procházka |
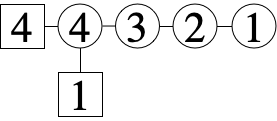
| Fig. 12.7: | The quiver of the bottom case should better be given as . |
Y. Pang |
| (A.1.8): | $a$ and $a_D$ on the right hand side should be reversed. | J.W. Kim |
| (A.1.9): | The first integral should be $\oint_B\lambda \oint_A \partial \lambda/\partial u$. | J.W. Kim |
| Two lines below (A.1.9): | $\partial \lambda/\partial u=-dz/(2xz)$ should be $\partial \lambda/\partial u=dz/(2xz)$. | J.W. Kim |
| (A.1.9): | $\partial \lambda/\partial u=-dz/(2xz)=dw + \cdots$ should be $\partial \lambda/\partial u=dz/(2xz)=-dw + \cdots$. | J.W. Kim |
email: yuji.tachikawa_at_****.**