ヤコビのθ関数は無限和表示と無限積表示があります。これには二次元の場の量子論による解釈があります。 質量の無い chiral boson と 質量の無い chiral complex fermion が(ほぼ)等価な理論なので、分配関数をボゾン側で計算すると無限和になり、フェルミオン側で計算すると無限積になる、というものです。
似たような話で、complex fermion 四つと、その $\mathbb{Z}_2$ orbifold の関係から, $$\frac{1}{2}\Bigl(\theta_{00}(a) \theta_{00}(b) \theta_{00}(c) \theta_{00}(d) - \theta_{01}(a) \theta_{01}(b) \theta_{01}(c) \theta_{01}(d) - \theta_{10}(a) \theta_{10}(b) \theta_{10}(c) \theta_{10}(d) + \theta_{11}(a) \theta_{11}(b) \theta_{11}(c) \theta_{11}(d)\Bigr) \\ = \theta_{11}\bigl(\frac{a+b+c+d}2\bigr) \theta_{11}\bigl(\frac{a-b-c+d}2\bigr) \theta_{11}\bigl(\frac{a-b+c-d}2\bigr) \theta_{11}\bigl(\frac{a+b-c-d}2\bigr)$$ というリーマンの恒等式がでたりもします。 このあたりの議論に必要な場の量子論は頂点作用素代数としてきちんとした数学になっています。
19 世紀から知られているモジュラー J 関数は $$J(q)=\frac1q + 196884q+21493760q^2 + 864299970q^3+\cdots$$ という展開を持ちますが、 20 世紀半ばになって、展開係数が散在型有限単純群の最大のものであるモンスター群の既約表現の次元を用いて $$\begin{aligned} 196884&=1+196883,\\ 21493760&=1+196883+21296876,\\ 864299970&=1+1+196883+196883+21296876+842609326 \end{aligned}$$ という分解があることが気がつかれました(Conway-Norton,1979)。 この観察の背後には、ある二次元カイラル共形場理論 = 頂点作用素代数でモンスター群の対称性をもつものの分配関数が J(q) になっているという事実があります。
この頂点作用素代数が構成されたのは1988年の Frenkel-Leopwsky-Meurman の本で、そもそもモンスター群の対称性をもつ数学的対象でもっとも自然なものはこの頂点作用素代数です。 数学者むけの論説ですが1999年の原田「モンスターの数学」というのがあります。
モンスター群と頂点作用素代数の上記の関係を知ると、二匹目のどじょうを探したくなるのは人情です。積極的に探したつもりではないのに見つかった例を紹介します。1989年に僕の兄弟子の大栗さんは、指導教員の江口さんとやった仕事を元にした博士論文で K3 曲面上を動く弦理論に付随する頂点作用素代数を考え以下の展開を得ました:
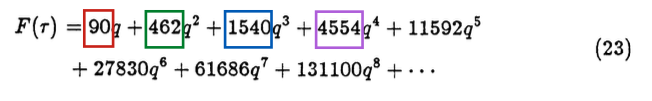
この係数には何か意味はないでしょうか? 当時数学者の向井さんにより K3 曲面の対称性はマチウ群という有限群の特殊な部分群であるということが知られていました。 20年たって、2009年にアメリカのアスペンの研究会に僕と江口さんと大栗さんが同時に参加していた際、ふとこの話が話題にのぼり、岩波数学辞典の付録にのっているマチウ群の既約表現の次元と比較をしてみました:

見事に関係があります!(色つきの箱を二つの図で比較してみてください。) モンスター群の場合と同様、適切な頂点作用素代数があって、そこにマチウ群 $M_{24}$ が作用していればいいのですが、それから 15 年経ったものの、ちょうどよい頂点作用素代数はみつかっていません。困ったことです。 2012 年時点でのレビューは僕の書いたこちらなどがあります。
これも同じ頃の話ですが、作用素環の研究者 Jones が 1985 年に結び目の位相不変量を発見しました。この不変量は結び目の平面への射影をつかって定義されており、定義から位相不変量であることを示す時点で一苦労です。 これについて三次元の場の理論を使えば位相不変量であることが明らかな「定義」ができるのではないか、と Atiyah が思い、Witten に聞いた所、Witten が SU(2) をゲージ群にもつ Chern-Simons 理論の Wilson loop の期待値が丁度 Jones 多項式になっていることを明らかにしたそうです。 (Atiyah が Witten に聞いたら,というところはどこかで読んだ気がしますが覚え違いかもしれません。 このエピソードは下の Donaldson 不変量のほうかもしれません。) その後も現代に至るまでこれに基づいた発展が沢山あります。
ちなみに非可換群 SU(2) のかわりに可換群 U(1) をつかうと古典的なガウスの絡み数 (linking number) が出ます。ガウスの絡み数というのは結局のところマックスウェル方程式の積分形で、磁場をループ上で積分すると、そのループを端に持つ面を横切る電流で与えられる、というもので、Jones-Witten のこの話はその非可換ゲージ群版になっているわけです。
Witten の原論文は1989 年のこちらです。 Witten 自身が 2011 年に一般向けにこれについて書いた記事もあります。
ちなみに、安直に場の量子論的に考えると、三次元チャーンサイモンズ理論は Atiyah-Segal 式の TQFT に大体なりそうに思えるのですが、三次元多様体の接束に枠(frame)を導入しないとうまく行かず、Chern-Simons 理論に関する初期の数学の論文はどれもそこの処理にかなりの労力をつかっています。 この接束の枠への依存性がすでに上記の Witten の原論文に書いてあるのは驚くべきことです。 枠への依存性は Chern-Simons 理論の 1 ループの摂動的解析からくるので、こういうところからも、場の理論の摂動論が数学においても重要であることがわかります。
さて、時間を二十年ほど溯ります。 量子異常というのは、(発見された当時の観点では)カイラルフェルミオンのラグランジアンに古典的には対称性があるけれども、 量子化するとその対称性が微妙に保たれず、保たれない具合が厳密に決定できるというもので、1970 年初頭にみつかりました。 非常におおざっぱには、古典的には保存されているカレント $j^\mu$ が保存されなくなるが、それが $$ \partial_\mu j^\mu \propto \epsilon^{\mu\nu\rho\sigma} F_{\mu\nu} F_{\rho\sigma} $$ となり、非保存をしめす右辺の係数まで厳密に決定できるという話です。 しばらくして、これが数学で1960年代に全く独立に発見された Atiyah-Singer の指数定理という定理とほとんど同じものであることがわかりました。
物理側では、パイオンの二光子崩壊のファインマン図による摂動計算の微妙なところから生じます。(上式の左辺がパイオンをつくるカレント、右辺に光子が二回あらわれます。) QCD の色の数が 3 であることの実験的確認のほぼはじめの例にもなっています。これは数学側の証明とは似ても似つかないものです。 この二つの関係を明らかにした初期の物理側の論文が 1979 年の藤川さんのもので、これは Atiyah-Singer と Atiyah-Patodi-Singer の論文を引用しています。
また、以前、物理側で量子異常の理論のおおざっぱなまとめの講演をした際のファイルがあるので紹介しておきます。そこではあまり数学との関係を明示しませんでしたが...
超対称性というのはフェルミオンとボゾンをいれかえる対称性で、現実の素粒子物理の観点からも興味が持たれ、深く研究されてきましたが、場の量子論と数学の関係においても重要な役割を果たします。といっても超対称量子力学はなんてことはなく、単にヒルベルト空間 V に固有値が $\pm1$ である演算子 $(-1)^F$ があり、それと反交換するエルミート演算子 $Q$ があり、ハミルトニアンが $H:=Q^2$ であたえらえる、というだけです。このとき $$ I(\beta):=\mathrm{tr}_V (-1)^F e^{-\beta H} $$ という量が $\beta$ に依存せず、さらに $Q$ の連続変形にも依らない、というのが Witten の観察で、この量は Witten index と呼ばれます。(ご本人は謙遜なさって決してそうは呼びませんが。)
中途半端な $\beta$ の値で上式を評価するのは困難ですが、$\beta\to0$ と $\beta\to\infty$ では計算できることがしばしばあります。この値は $\beta$ に依存しないはずですから、$I(0)=I(\infty)$ が得られますが、これは非自明な式になることがしばしばあります。
さて、超対称でなくてよい普通の場の理論をとり、四次元時空 $M$ 上のフェルミオンでゲージ場に結合しているラグランジアンを書き、フェルミオン波動関数の空間を $V$、そこに働く$\gamma^5$ を $(-1)^F$, ディラック演算子 $D$ を $Q$ と取ると、ここには超対称量子力学の構造があります。ここで上式 $I(0)=I(\infty)$ を書き下すと、指数定理、おなじことですが量子異常の式が出てきます。導出を振り返ると、上で紹介した藤川さんの方法と実質同じであることがわかります。
大切なことなので繰りかえしますが、四次元の場の理論としては超対称でなくても、フェルミオンがあるだけで、その一粒子状態には超対称性の構造があり、それが理論の構造をあきらかにしてくれるわけです。ただ、この段階では、超対称性によって数学で新たなことがわかったことにはなりません。1980年代前半の話です。
Witten 指数に関しては(量子異常との関係ではない文献ですが)ご本人の1982年の原論文をお薦めします。 他の人の書いたレビューよりよほど判りやすいです。
フェルミオンの量子異常は数学ではディラック演算子に対応する Â 種数とよばれる量に対応しますが、他の演算子に対応する様々な別の種数があります。 数学者はその中でも楕円種数 (elliptic genus) と呼ばれる一連の種数が特別な性質をもつことに気付きました。 この性質は、楕円種数を二次元の超対称場の理論の Witten index と考えると説明がつくことを示したのが Witten の 1987 年のこの論文です。
一般に、$d$ 次元の超対称場の理論で、時空が $M_{d-1}\times S^1$ の形をしていると、時刻一定面が $M_{d-1}$ であるときのヒルベルト空間を $V$、フェルミオンパリティを $(-1)^F$、$S^1$ 方向の超並進を $Q$ とすると、超対称量子力学の構造を持ちます。(量子力学は 0+1 次元の場の量子論ですから、$d$ 次元の場の理論を $M_{d-1}$ 方向にコンパクト化して 1 次元の場の量子論を得たわけです。)するとその Witten index を考えられる、というわけです。 $d=2$ として $M_1=S^1$ としたのがこの場合です。以下、他の $d$ で他の $M_{d-1}$ を選んだ話が何度も出てきます。
この論文以降、数学では楕円種数の研究は物理とは独自に進み、楕円コホモロジー、さらに位相的モジュラー形式として完成します。 一方、物理側では数学側の楕円種数の研究は顧みられることが(2015年ごろまで)なく、単に二次元超対称場の理論の Witten index を(数学との関係を忘れて) elliptic genus と呼ぶ状態が数十年続きます。
四次元多様体の微分構造について 1983 年に Donaldson が多様体上の SU(2) 接続の反自己双対方程式のモジュライ空間、物理側の言葉ではインスタントンを調べることによってそれまで予期しなかった種々の結果を示しました。 これも場の量子論の言葉で再解釈できないか、と思ったのが Atiyah だったか Witten だったかわかりませんが、それを実現したのが Witten の 1988 年のこの論文で、そこでは四次元の N=2 超対称ゲージ理論という理論の限定されたクラスの演算子の相関関数を計算すると、ちょうど Donaldson 不変量になる、ということが示されています。 上で超対称量子力学や、より一般に場の量子論を $M\times S^1$ という形の時空で考えると、Witten index が 理論のパラメタに依存しない量になり、いろいろ数学的な情報が取り出せると書きましたが、 これは時空の形が $S^1$ との直積でなくとも、関連するが別の方法で結果が理論のパラメタの連続変形に依存しないことが示せる、というものです。
その時点では、単に数学の結果を場の量子論の言葉に書き直しただけでしたが、その後 1994 年に Seiberg-Witten が N=2 SU(2) 理論の長距離極限が N=2 U(1) 理論に帰着することを示し(物理の側の Seiberg-Witten 理論)、それを用いると多様体上の U(1) 接続をもちいた Seiberg-Witten 不変量が定義でき、 超対称性の一般論から Seiberg-Witten 不変量には Donaldson 不変量に含まれている情報が全て含まれているだろう、ということになります。 U(1) 接続は SU(2) 接続より数学的にも断然調べやすいですから、ここから四次元微分幾何のさらなる発展がありました。
このあたりは以前「物理と数学の Seiberg-Witten 理論」という動画を準備したので是非ご覧ください。 物理編、 数学編です。 手書きのノートもあります。
ちなみに Seiberg-Witten 不変量はさらに数学側では Bauer-Furuta 不変量というものに進化/深化しているのですが、これをまだだれも物理側に再輸入していないようです。将来的には考えてみたいテーマです。
まずは以下の図をみてください。(この観察をはじめてした論文ではなく、比較的最近のこの論文から Fig.3(a) を借用しました。)
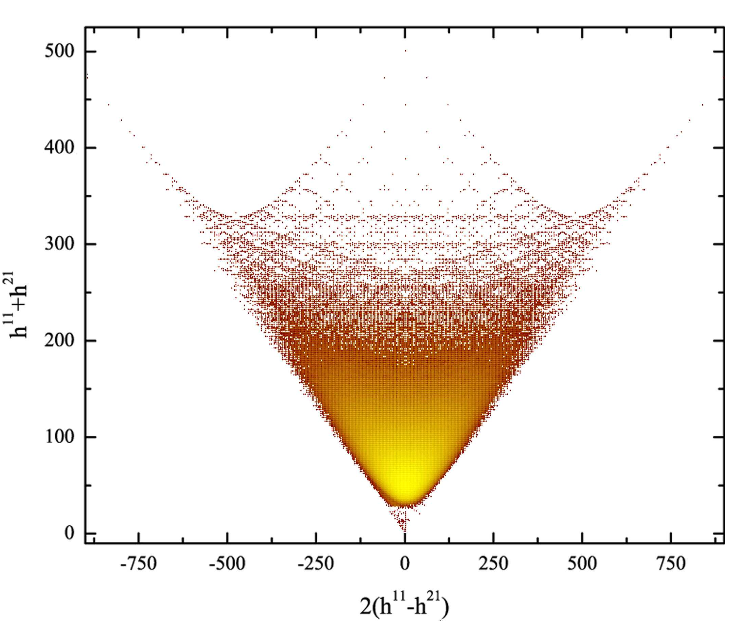
これは既知の複素三次元(実六次元)のカラビヤウ多様体のホッジ数 $h^{1,1}$ と $h^{2,1}$ をプロットしたものですが、$h^{1,1}$ と $h^{2,1}$ の入れ替えに対して対称性があるように見えます。$h^{1,1}\leftrightarrow h^{2,1}$ で結びついている互いにミラーな多様体があるとするとよさそうです。
これが見つかった経緯ですが、超弦理論は10次元で、この世は4次元ですから、残りの6次元をコンパクト化しないといけません。このときカラビヤウ多様体を使うのが都合が良いことが1980年代半ばにわかりました。すると、カラビヤウ多様体をターゲットとする二次元超対称場の理論を考える必要があります。
カラビヤウ多様体 $M$ から二次元超対称場の理論 $\sigma(M)$ を作ると、自然に N=(2,2) 超対称共形場理論というものになりますが、一般に N=(2,2) 超対称共形場理論全体の空間には簡単な操作 $T \mapsto m(T)$ で $m^2(T)=T$ となる操作があります。(二つの $U(1)_R$ 対称性を入れ替える操作です。) また、$T$ に対して、$h_A(T)$, $h_B(T)$ という非負整数があり、 $h_A(m(T))=h_B(T)$, $h_B(m(T))=h_A(T)$ を満たします。 さらに、特に $T=\sigma(M)$ なら、$h_A(\sigma(M))=h^{1,1}(M)$, $h_B(\sigma(M))=h^{2,1}(M)$ です。
さて、ここで二つのカラビヤウ多様体 $M$, $W$ に対して $$ m(\sigma(M))=\sigma(W), \quad \sigma(M)=m(\sigma(W)) $$ だとしましょう。 すると、上の関係から、$h^{1,1}(M)=h^{2,1}(W)$、また $h^{2,1}(M)=h^{1,1}(W)$ が自然と従います。
同様に,$T$ に付随した複素関数 $F_A$, $F_B$ で $F_A(m(T))=F_B(T)$、$F_A(T)=F_B(m(T))$ を満たし、 $F_A(\sigma(M))$ は $M$ のグロモフ=ウィッテン不変量( $M$ 内の球面の数を数えて得られるもの)、 $F_B(\sigma(M))$ は $M$ の周期積分( $M$ で正則(3,0)-形式を積分して得られるもの)、となるものがあります。 すると $M$ のグロモフ=ウィッテン不変量という代数幾何の数え上げ問題が $W$ の周期積分で得られる、ということになります。 これをはじめて指摘した論文が 1990 年代初頭のこちらです。 これにはじまる数学者とのやりとりは僕の講演の真ん中辺りでもとりあげました。
さらに、$T$ に付随したカテゴリ $C_A$, $C_B$ で、 $C_A(m(T))=C_B(T)$、$C_A(T)=C_B(m(T))$ を満たし、 $C_A(\sigma(M))$ は $M$ の連接層の導来圏、 $C_B(\sigma(M))$ は $M$ のシンプレクティック構造から定まる深谷圏、となるものがあります。 すると、$M$ の連接層の導来圏が $W$ の深谷圏と等価であるべし、というホモロジー的ミラー対称性が出るわけです。
二次元 N=(2,2) 超対称共形場理論を抽象的に扱う段階では、ミラー操作 $T\mapsto m(T)$ はかなり自明な操作です。一方、カラビヤウ空間 $M$, $W$ に対し対応する二次元 N=(2,2) 超対称共形場理論が $m(\sigma(M))=\sigma(W)$ を満たすというのは $M$ と $W$ に対してとても非自明な操作です。どこが難しいかというと、カラビヤウ多様体 $M$ から場の量子論 $\sigma(M)$ を構成し、これが二次元 N=(2,2) 超対称共形場理論である、という段階です。これは物理側でも、二次元超対称シグマ模型の繰り込みに伴う微妙な議論を必要とします。物理側でこういう数学者にはわかりにくい操作をするからこそ、 数学側で非自明な結果がでてくるわけです。
これはこのリストのなかでも特に僕が慣れていない内容で、嘘を書いたらすいませんが、1990年ごろ、弦理論屋さんは二次元重力を色々な方法で調べていました。その中で、行列模型という行列の積分を用いた方法と、トポロジカル重力という方法とが、同じ結果を与えるらしいということが判ってきました。行列模型は一番簡単なばあいはしばらくして解かれ、可積分系として有名な KdV 方程式系によって記述されることがわかりました。(同時期にいろいろ論文があったらしいですが、一つは1990年のこれです。)一方で、トポロジカル重力の計算は、リーマン面のモジュライ空間上で Mumford-森田類というコホモロジー類の積を積分したものになることがわかります。これを組み合わせると、リーマン面のモジュライ空間上の交叉理論が KdV 方程式系で記述されるべき、という数学だけからみると驚くべき予言に至ります。
この予言を書き下したのが Witten の1990年の論文で、証明したのは Kontsevich の1991年の論文で、その後、この関係式には色々な拡張もみつかっています。
この話がこのリストの他の項目と少し違うと(僕が)思うのは、次の点です。 他のものは場の量子論側を物理屋としてよく理解していれば、当然数学的予言が成り立たつはずだとわかるようなものになっています。 しかし、この関係式に関しては、少なくとも Witten が予想をたてた時点では、場の量子論側でも二次元重力の二つのモデル(行列模型とトポロジカル重力と)が同じであるという理解には達していなかったと思うわけです。まあ、それなのに等価であると喝破した Witten はそれだけ偉い、ということかもしれませんが。
その後の長い弦理論の発展で、これは AdS/CFT 対応などの重力理論とゲージ理論の対応、別名では閉弦-開弦対応の一番簡単な例でしかも数学的に証明できる例になっていることがわかっていたはずです。
Maxwell 方程式において磁場の満たす式と電場の満たす式がほとんど同じことはご存知かと思います。 Maxwell 理論はゲージ群が U(1) のゲージ理論で、ゲージ群を非可換群にしたのが Yang-Mills 理論ですが、 Yang-Mills 理論では磁場の満たす式と電場の満たす式は完全に同じではありません。 しかし 1977年、Goddard, Nuyts, Olive は、ゲージ群が $G$ の Yang-Mills 理論の磁気的励起のスペクトルは、 一般には別のゲージ群 $G'$ の Yang-Mills 理論の電気的励起のスペクトルと非常に似ていることに気がつきました。 $G'$ を $G$ の GNO 双対といいます。 $U(1)$ の GNO 双対が $U(1)$ 自身であるから Maxwell 方程式は磁場と電場の入れ替えで不変だったわけです。
その少し前,数学者のラングランズは 1970年代前半に、数論の考察から同様に群 $G$ に対して双対群 $\widetilde G$ を対応させると色々良いことがあることに気がつき、それを用いて数論のラングランズ・プログラムというのを提唱しました。 (こちらの話の初期の状況については IAS のこのページに私信もふくめて詳細にまとまっています。) $\widetilde G$ は $G$ のラングランズ双対と呼ばれます。 ここで不思議なのが、$G$ の GNO 双対 $G'$ とラングランズ双対 $\widetilde G$ は同じものであることです。
さて、物理のほうの1993年ごろの発展を説明しましょう。 $G$ に対して N=4 最大拡大超対称ゲージ理論という場の量子論を考えることができます。この理論を $X(G,e)$ と書きましょう。ここで $e$ は結合定数です。すると、場の量子論として、 $X(G,e)$ と $X(G',e')$ は似ているだけでなく、$e=1/e'$ として完全に等価である、すなわち $$ X(G,e) = X(G',1/e) $$ が判ってきました。ただし、等号の左右で電場と磁場を入れ替えるものとします。 場の量子論の摂動的な研究では、$e$ に関してテーラー展開しますから、 場の量子論間のこの等式は摂動論では得られないものです。これを S 双対と言います。 これは当時の研究者には非常な驚きだったとのことです。(たとえば Witten 先生のインタビュー に詳細に出てきます。) また、この関係式は純粋に場の量子論の研究から出てきたのではなく、当時の弦理論業界全体の研究で、弦理論自体に $e\leftrightarrow e'=1/e$ なる対称性があることがわかってきたもので、その中で場の理論で扱いうるサブセクターを取り出すことによって発見されたものだった、と指摘しておきます。
この四次元の場の量子論の間の等式がありますので、両辺を二次元空間かけるリーマン面 $\Sigma$ で考察すると、$\Sigma$ に依存する二次元の場の量子論間の等式が得られます。これに対して二次元のミラー対称性(の類似)を考えるとラングランズ対応の(もともとは数論的な話だったところを)幾何学化したものが得られる、というのが場の量子論からのラングランズ対応へのアプローチです。 しかし N=4 超対称ヤンミルズの S 双対性から出てくる数学はこれに留まるものではなく、その他の色々なあらわれがあります。
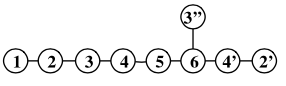
単純リー環はディンキン図で分類できるのはよく知られています。 特にディンキン図で二本線、三本線をつかわないものを simply-laced と言い、$A_n=su(n+1)$、$D_n=so(2n)$、$E_{6,7,8}$ で尽きます。 $E_8$ の拡大ディンキン図を下に掲げました。中に書いてある数字は Dynkin (co)mark と呼ばれるリー環論で重要な量です。
一方、$SU(2)$ の有限部分群は、2:1 の写像 $SU(2)\to SO(3)$ によって、三次元空間の回転の有限部分群、すなわち正多面体群にうつることを用いて分類でき、 単なる回転のなす $\mathbb{Z}_n$、正二面体群をもちあげた $\widehat D_{n}$, 正四面体群をもちあげた $\widehat T$, 正八面体群をもちあげた $\widehat O$, 正二十面体群をもちあげた $\widehat I$, で尽きます。
両者の分類とも、ふたつの無限系列があり、例外的なものがみっつある、という不思議な符合がありますが、それだけではないことに McKay が気がつきました。 すなわち、$\Gamma\subset SU(2)$ を有限部分群とし、 $\Gamma$ の既約表現 $\rho_i$ ごとに丸を書き、 $V$ を $\Gamma\subset SU(2)$ から定まる二次元表現とし、 $\rho_i$ と $\rho_j$ のあいだに一本線を $\rho_i\otimes V$ に $\rho_j$ が含まれるときのみ引くことにすると、 ちょうど対応するディンキン図が得られるのです。 上の $E_8$ の場合ならば、対応して有限群 $\widehat I$ には九つの既約表現があり、$V$ とのテンソル積の既約分解が上の図のようになっているわけです。 既約表現の次元が Dynkin (co)mark になっています。
(初出は1979 年の研究会報告集中の "Graphs, singularities, and finite groups" という論文です。 McKay がこれに気付いた経緯は数学セミナー2012年9月号の松澤さんの記事「空間の点群・結晶群と有限性/マッカイ対応とSL2,SL3の有限部分群」に本人から聞いた話が載っています。興味深いので是非みてください。 ちなみに上の項目で述べた J 関数の展開係数とモンスターの表現の次元の関係にはじめに気付いたのも、上で引用した Conway-Norton によれば McKay だったそうです。 不思議な関連に気付く人だったようです。)
さて、この関係はまあ数学的事実だからしょうがないのですが、$SU(2)$ の有限部分群 $\Gamma$ と対応する単純リー環 $\mathfrak{g}$ もしくは対応するコンパクトリー群 $G$ の間にもっと直接的な関係はないのか、というのが気になります。 これが超弦理論内にみつかったのが 1990 年代半ばで、M 理論や Type IIA 超弦で、 $\mathbb{C}^2/\Gamma$ という特異点があるばあい、その特異点上に $G$ ゲージ理論が生じる、ということになっています。
これだけだと数学への寄与はないわけですが、下で出てくる項目の準備として必要です。
四次元多様体上の半自己双対接続=インスタントンのモジュライ空間の幾何をしらべることで四次元の微分幾何がよく分かったというのが Donaldson の進展でした。 もっとも安直な四次元多様体である $\mathbb{R}^4$ 上のインスタントンのモジュライ空間ですら面白い構造をもち、量子色力学の閉じ込めとの関連も想定されたため、物理学者がいろいろな具体的なインスタントン解をみつけましたが、結局四人の数学者 Atiyah, Hitchin, Drinfeld, Manin が有限サイズの行列数個を用いてもっとも一般の解の構成に成功しました。これが1978年の ADHM の論文です。 (冷戦のまっただ中で、西側の Atiyah-Hitchin と東側の Drinfeld-Manin が独立に発見したことにお互いが気付き、共著で論文を書いたということ自体も素敵な話ですが、閑話休題。)
ただ、結果は簡単ではあるものの、物理屋からすると何故これで答えがでるのかしっくりこないというのが長らく続いたのではないかと思います。これが物理屋(の中の少なくとも弦理論屋)にすっきりわかったのは1990年代半ばに D-brane の理解が進んだときです。 すなわち、$N$ 枚の D($p+4$)-brane の中に、$k$ 個の D$p$-brane は、$U(N)$ ゲージ理論の $k$-インスタントン解として溶け込むことができるのですが、 一方この brane 系にごく普通に開弦の量子化を適用してやると、ちょうど ADHM が使った有限個の行列の自由度が生じ、それらの行列に ADHM が課した条件も自然にこの brane 系 の超対称性を保つ真空の条件として得られるのです。
この話の一般化もあります。1990年の Kronheimer-Nakajima の論文で、ADHM 構成が、$\mathbb{C}^2/\Gamma$ をブローアップした空間上での $U(N)$ インスタントンのモジュライ空間の構成に拡張されていますが、 これも D($p+4$)-brane を $\mathbb{C}^2/\Gamma$ に置き、これに D$p$-brane でプローブすれば、開弦の量子化から自然に理解できることが知られています。Douglas-Moore の1996年の論文です。
これもこれだけでは数学への寄与がありませんが、下の項目の準備として必要です。
上記 ADHM 構成も、Kronheimer-Nakajima 構成も、ハイパーケーラー商という、$G$ 作用のある線形ハイパーケーラー空間 $V$ から非自明なハイパーケーラー多様体 $V///G$ を作り出す構成の例になっています。 このハイパーケーラー商構成は、$V$ と $G$ から定まる三次元 N=4 超対称理論 $S(G,V)$ の超対称真空の一部であるヒッグス枝 $\mathrm{Higgs}(S(G,V))$ であるということが1987年から知られています。
さて、三次元 N=4 超対称理論 $T$ 全般を考えることにしますと、 二次元のミラー対称性の類似として(二つの $SU(2)_R$ 対称性を交換することから従う)簡単な操作 $T\mapsto m(T)$ で、$m^2(T)=T$ であるものがあり、 $T$ に対してその超対称真空から取り出せる二つのハイパーケーラー多様体 $\mathrm{Higgs}(T)$ と $\mathrm{Coulomb}(T)$ があり、 $\mathrm{Higgs}(m(T))=\mathrm{Coulomb}(T)$, $\mathrm{Higgs}(T)=\mathrm{Coulomb}(m(T))$ となっています。 よって、$S(G,V)=m(S(G',V'))$ だったとすると、$$ \mathrm{Higgs}(S(G,V))=\mathrm{Coulomb}(S(G',V')),\qquad \mathrm{Higgs}(S(G',V'))=\mathrm{Coulomb}(S(G,V)) $$ となるはずです。 $\mathrm{Higgs}(S(G,V))$ のほうはハイパーケーラー商構成として1980年代後半から知られていることは既に述べました。 $\mathrm{Coulomb}(S(G,V))$ の数学的構成は比較的最近で、2015年の中島さんの論文からはじまるものです。 これにより、ハイパーケーラー多様体間の等式が色々得られます。
もうひとつの応用として、M 理論を $\mathbb{R}^7\times \mathbb{C}^2/\Gamma$ で考え、 これを $k$ 枚の M2-brane で probe することを考えます。 これは三次元 N=4 超対称理論になりますが、 上の Douglas-Moore の論法をつかうと具体的に $$S(\prod_i SU(k N_i),V)$$ の形で書き下せます。 ここで $N_i$ は $\Gamma$ に対応するディンキン図の (co)mark で、 $V$ は Dynkin 図の辺から定まります。 さて、上の議論から $\mathbb{R}^7$ 上には $\Gamma$ に対応する simply-laced な群 $G$ のゲージ場が生じ、もうすこし考えると $$ \mathrm{Coulomb}(S(\prod_i SU(k N_i),V)) $$ が $G$ の $k$-instanton モジュライ空間であるべし、ということがわかります。 例えば、$G=E_8$、対応して $\Gamma=\widehat I$ として、それに中島さんの構成を適用すると、 上に示した Dynkin 図のデータから $E_8$ の $k$-instanton モジュライになっているはずです。 ADHM 構成は古典群のインスタントンモジュライしか作れませんから、 ここまでくると場の理論/弦理論の考察からハイパーケーラー空間に対する新たな予想が得られたことになります。
すこし別の話をしましょう。四次元 N=1 超対称ヤンミルズ理論はゲージ群 $G$ を指定すれば定まります。これは現実の素粒子論の「強い力」を記述するヤンミルズ理論と同様、閉じ込めを起こすと信じられています。短距離ではほぼ自由なグルーオンの理論で、長距離では閉じ込めて質量ギャップのある理論です。
そこで、理論をサイズ $L$ の三次元トーラス $T^3$ かける時間方向 $\mathbb{R}$ で考えましょう。上のほうの議論と同様、この系の Witten index $I(G,L)$ を考えることができます。 長距離 $L\to \infty$ では閉じ込めた描像で計算し、$I(G,L\to \infty)=h^\vee(G)$ を得ます。ここで $h^\vee(G)$ は双対コクセター数という、リー群の理論で重要な量です。 短距離 $L\to 0$ では自由なグルーオンの描像で計算し、$ I(G,L\to 0) = \sum_i (1+ \frac13\dim_{\mathbb{R}} M_i) $ となります。ここで $M$ は交換する三つ組みのモジュライ空間、すなわち $$ M=\{ g_1,g_2,g_3\in G \mid \text{$g_{1,2,3}$ は互いに交換}\} / \sim $$ ただし $$ (g_1,g_2,g_3)\sim (h_1,h_2,h_3) \quad \text{iff}\quad k(g_1,g_2,g_3)k^{-1}=(h_1,h_2,h_3) \quad \text{for some $k\in G$} $$ として、 $M=\bigsqcup_i M_i$ を連結成分への分解としました。 Witten index は $L$ に依存しませんから、ヤンミルズ理論の閉じ込めという実験事実から $$ h^\vee(G) = \sum_i (1+ \frac13\dim_{\mathbb{R}} M_i) $$ という不思議な等式が得られました。
この等式は $G=SU(N)$ の場合はWitten index の物理側のほぼはじめの1982年の論文でやってあり、 $G=Spin(N)$ の場合がやはり Witten によって1997年の論文の付録でなされました。 一般の場合は数学者三人の1999年の140ページの論文で示されています。
これに関しては僕が 2014 年にした講演のファイルもあります。また交換する三つ組みのモジュライ空間は McKay 対応およびラングランズ/GNO双対と組み合わせることで不思議な関係も導きます。それに関しては僕の 2015 年のまた別の講演ファイルをご覧ください。
次に四次元 N=1 超対称 QCDを考えます。色の数が $N_c$、クォークの種類が $N_f$ だとします。このとき、超対称でない現実の QCD の閉じ込めに類することが起こりますが、何が起こるかは $N_c$ と $N_f$ の詳細によります。 たとえば、$N_c=2$ で、$N_f=3$ のときは、高エネルギーはゲージ理論ですが、低エネルギー極限は単にバリオンが六つ、メゾンが九つ、合計 15 個の自由場で書かれると思われています。(これは Seiberg の 1994 年ごろの結果です。)
ここで理論を $S^3\times S^1$ で考え、Witten index を計算します。$S^3$ が小さいときは、高エネルギー極限のゲージ理論で計算し、$S^3$ が大きいときは、低エネルギー極限の自由場で計算します。Witten index はサイズに依存しませんので、等式が得られます。具体的に書き下すと、$$ \frac12\oint \frac{dz}{2\pi iz} \underbrace{\frac{1}{\Gamma_{ty,t/y}'(1) \prod_{\pm} \Gamma_{ty,t/y}(z^{\pm2})}}_\text{ゲージ場の寄与} \underbrace{\prod_{\pm,i} \Gamma_{ty,t/y}(t^{1/3} z^{\pm1} \mu_i\nu)}_\text{クォークの寄与} \underbrace{\prod_{\pm,i} \Gamma_{ty,t/y}(t^{1/3} z^{\pm1} \frac{\widetilde\mu_i}{\nu})}_\text{反クォークの寄与}\\ = \underbrace{\prod_i \Gamma_{ty,t/y}(t^{2/3}\mu_i^{-1}\nu^{2} )}_\text{バリオンの寄与} \underbrace{\prod_i \Gamma_{ty,t/y}(t^{2/3}\widetilde\mu_i^{-1}\nu^{-2} )}_\text{反バリオンの寄与} \underbrace{\prod_{i,j} \Gamma_{ty,t/y}(t^{2/3}\mu_i\widetilde\mu_j )}_\text{メソンの寄与} $$となります。ただし$$ \Gamma_{p,q}(x)=\prod_{m,n}\frac{1-z^{-1} p^{m+1}q^{n+1}}{1-z p^m q^n} $$ は楕円ガンマ関数と呼ばれる特殊関数です。
このように N=1 超対称 QCD の $S^3\times S^1$ の Witten index から等式を書き下すというのをはじめて行ったのが2005年の Römelsbergerの論文です。
この等式自体は数学で楕円ガンマ関数の専門家によって以前から知られていたもの(のはず)ですが、四次元の N=1 超対称ゲージ理論の強結合領域での振る舞いで同様にわかっているものはその他にも多数あり、その一つ一つから、同様の楕円ガンマ関数沢山の積の複素積分の間の不思議な等式が予言されます。そうやって予言された式の大部分は数学的な証明はまだついていないというのが現状です。 物理側のレビューは僕が書いたこちらの Chapter 7 をお薦めします。 楕円ガンマ関数の専門家の数学者が書いたレビューもあり、多少古いですが2009年のこちらはどうでしょうか。
ここまで見てきた例を抽象すると、
- ある次元 $d$ の超対称場の理論 $T$ に対して、数学的な対象 $h$ を対応させる手続き $T\mapsto h(T)$ があり、
- また、何らかのデータ $D$ からその次元の超対称場の理論 $T(D)$ を作ることができ、
- $h(T(D))$ は $D$ から(場の理論という未定義なものを含まない)数学的な手続き $t(D)$ で書けるとし、
- さらに、異なるデータ $D$ と $D'$ に対し双対性 $T(D)=T(D')$ であることが知られている
場の理論的にも、1, 2, 3 はそれほど難しくないのですが、一番の問題は、4 を満たす D, D' のペアをどのように作るか、ということにあります。 ここは長年名人芸のようにすこしずつ見つかっていたのですが、2009 年の Gaiotto の class S 理論により、大量に一気に作る方法がみつかりました。 基本的には、六次元の N=(2,0) 超共形場理論というものをとり、それを(追加情報つきの)リーマン面 $\Sigma$ でコンパクト化して得られる四次元の N=2 超対称理論を考え、ひとつの $\Sigma$ の異なるパンツ分解を $D$, $D'$ としたとき $T(D)=T(D')$ となる、というものです。 四次元 N=2 超対称理論からは沢山計算できる数学的な対象 $h$ がありますので、この方法で大量に数学的に予言が得られます。
これについては2009年ごろから10年ほど僕の主な研究内容でしたので、沢山説明を書きました。ある程度数学者向けに書いたものは長い版と短い版とがありますので、そちらをご覧ください。 その中に出てくる個別の例を説明すると、このウェブページに書いてある例全体より長くなりそうなぐらいです。
ここまでみてきた場の量子論と数学の関係においては、場の量子論は自由場であるか超対称場の理論であるかどちらかで、純粋に場の理論的な考察をしてばかりでした。 一方、1997 年以降の超弦理論の発展では、AdS/CFT 対応という、$d$ 次元の場の量子論(主に共形場理論(CFT)ですが)が $d+1$ 次元のアンチドジッター(AdS)空間上の重力理論と等価であるという関係が非常に重要です。 こちらは量子重力理論という、場の量子論よりさらに数学的整備が遅れている分野が関連するため,そこから取り出された数学は少ないですが、無くはないです。
たとえば、四次元 N=1 超対称共形場の理論を沢山つくる方法として、 Type IIB 超弦を $\mathbb{R}^4$かける実六次元(複素三次元)のカラビヤウ錐で考え、 そこに D3 ブレーンを沢山導入する、という方法があります。これの重力双対は、 カラビヤウ錐が五次元のコンパクトな空間 $Y$ の上の錐だとして、$AdS_5\times Y$ 上の Type IIB 理論で与えられます。 奇数次元の空間 $Y$ の上の錐がケーラー多様体のとき $Y$ を佐々木多様体、$Y$ の上の錐がカラビヤウ多様体のとき $Y$ を佐々木アインシュタイン多様体と言います。 佐々木(アインシュタイン)多様体はもちろん数学者独自の興味から以前から調べられていたのですが、この関係から研究が再燃するということがありました。
たとえば、佐々木多様体 $Y$ には Reeb ベクトル場というものが存在します。($Y$ の上の錐がケーラー多様体なので、$Y$ の錐の方向に $i$ をかけて得られる方向がかならず $Y$ 上のベクトル場を定める。)この Reeb ベクトル場の軌跡が閉じるかどうかは基本的な問題ですが、弦理論屋の2004年の論文で、はじめて Reeb ベクトル場の軌跡が閉じない佐々木アインシュタイン多様体がみつかりました。 また、与えられた佐々木多様体上にいつアインシュタイン計量が存在して佐々木アインシュタイン多様体になるかというのも数学的に基本的な問題ですが、これにも弦理論からの示唆があった後、数学的な解決に至っています。
日本語での初期の物理側のレビューは 2007 年の山崎さんのこちらなど、日本語での数学側の記述は「数学」誌の二木さんの2008年の記事と2012年の記事 をご覧ください。
残りの三つはこれまでとは毛色がちがい、理論物理側での分類問題に関するものです。 まずは超弦理論の D ブレーンの分類について考えます。
超弦理論は1980年代半ばに 1+1 次元的な弦の理論として定式化されましたが、 1990年代半ばになって、自然に 1+1 次元的だけでなく p+1 次元的な物体、「ブレーン」を含むことが認識されました。ブレーンにも何種類かありますが、もっとも普通のものが D-ブレーンというものです。 すると、時空 $X$ 上で超弦理論を考えた際に、その上の D ブレーンを連続変形を除いて分類せよ、というのは自然な問題です。 超弦理論にも何種類かあり、D-brane を含むものは Type IIA, Type IIB, Type I の三種類ありますから、それぞれに対して分類問題が立てられます。 D-brane は $p$ 次元的なところに巻いている何かですが、D-brane 上にはゲージバンドルも住んでいるので、それも含めて分類しないといけません。
結論は、K 理論を用いて,Type IIB なら $K^0(X)$,Type IIA なら $K^1(X)$、Type I なら $KO^0(X)$ で与えられる、ということになります。 レビューは 2000 年の Witten のこれがわかりやすいと思います。 ここでは K コホモロジーを使いましたが、K ホモロジーを使うこともでき、その場合は 1982 年の Baum-Douglas によるものがちょうど D-ブレーンに合致したモデルになっており、本当に部分多様体上のゲージバンドルを使うものになっています。
これだけなら弦理論の研究に数学を使った、というだけですが、弦理論では $X$ 上に計量だけでなく他の色んな場、たとえば 3-形式場 $H$ がある場合も考察し、対応して $K^*_H(X)$ などの捩れ K 理論とよばれるものも出てきます。$(X,H)$ 上のType IIA 理論が $(X',H')$ 上の Type IIB 理論と等価である、ということはしばしば起こり、すると $$ K_H^0(X) \simeq K_{H'}^1(X') $$ という、異なる空間で異なる捩れがある K 理論の間の等価性が予言されます。 このため捩れ K 理論の研究が盛んになりました。これに関しては数学側からの2012年のレビューがあります。
2010年ごろから、物性理論で symmetry-protected topological phase (SPT 相) というものに興味が持たれるようになりました。 同じ頃、トポロジカル絶縁体とかトポロジカル超伝導体と呼ばれるものも盛んに研究されました。 最近はトポロジカル物性が流行りですが、上記の二つはトポロジカル相の中でも特に簡易なもので、空間方向が閉じている場合の最低エネルギー状態の個数が一つである、という条件をみたすものです。こういうものを最近は可逆相といいます。 対称性のタイプを固定した際に、可逆相を分類しよう、というのが、手が届くかつ面白い問題として浮上したわけです。 自由フェルミオンの場合の分類は $K$ 理論と $KO$ 理論でなされることがすぐにみいだされ、「トポロジカル絶縁体/超伝導体の周期表」として知られるようになりました。
相互作用の効果を含めたときにどうなるか、というのの解決には時間が掛かりましたが、 結局、ボルディズム群のアンダーソン双対が分類になる、ということで決着をみています。 また、可逆相の表面には量子異常を持つ表面状態が住むことが認識され、逆に、 一般に $d$ 次元の場の理論の量子異常というのは対応する $d+1$ 次元の可逆場の理論で記述される、ということがわかったので、これにより 量子異常の一般論が完成しました。 このあたりは場の量子論による数学よりは場の量子論のための数学に近いですが、 上のほうの項目との関連で書いておくことにしました。
最後に、topological modular forms (TMF) の話をしましょう。 上で1980年代に楕円種数というのが数学で導入され、Witten によって二次元超対称場の理論による解釈が与えられたと言いました。その後、このテーマは物理側と数学側で長らく別々に研究されてきました。 数学側の進展としては、2002年頃に楕円種数および楕円コホモロジーの親玉として Hopkins により TMF が構成されたのが画期となります。 TMF は純粋にホモトピー論的には、通常のホモロジーを 0 番目, K 理論を 1 番目としてその次の 2 番目に自然に出てくるものですが、K 理論がベクトルバンドルの分類から出てくるような、自然な幾何学的な構成がないのが問題でした。
さて、K 理論の定義のひとつに、フレドホルム作用素を用いたものがありますが、それはすこし読みかえると、可能な超対称量子力学全体を、連続変形の元で分類している、と読むことができます。これに示唆されて、2004 年に Stolz と Teichner は
TMF $\simeq$ 二次元 N=(0,1) 超対称理論を連続変形で分類したものという予想を立てました。(この予想が提唱されてすぐの Teichner の講演とStolz の講演に僕は出席していたのですが、当時の僕には何もわからなかった記憶があります。) この予想は 2018 年ごろから物理屋にもとりあげられはじめ、僕も研究に参加しいくつか論文を書き、調べれば調べるほど確からしいという感触を得ています。
この関係は、数学側でわかっていることと物理側でわかっていることが相補的なため、お互いの知識を利用して相手側の理解を深めることができる、面白いものです。また、上のほうで議論した、場の理論の性質から数学的性質が導かれる,という場合と次のような大きな違いがある気がしています。
上で議論したようなケースでは、現時点では場の理論が未定義だから数学的な証明にはなっていないけれども、場の理論が定義され、場の理論側の性質が証明されれば、自然にそれが数学的性質の証明になっていると期待できます。 一方、この TMF との関係の場合は、上式で右辺にあらわれる場の量子論の概念がきちんと定義されたとしても、 左辺である TMF の数学側での定義とは大きく隔たりがある(例えば、右辺は本質的に $\mathbb{R}$ 上もしくは $\mathbb{C}$ 上の話だが、左辺は $\mathbb{Z}$ 上や正標数 $p$ を用いる)ため、等価性の証明にはさらに何か重要な一手が必要になると思われます。これも、僕にとってこの問題が特に面白い理由です。