宇宙観測検出器と量子ビームの出会い。新たな応用への架け橋。

研究課題 A02-1	仮想光子を使った ｎｎ 散乱長の精密測定による荷電対称性の破れの研究
研究代表者	石川 貴嗣 (東北大学)

概要： 「荷電対称性」は強い相互作用がもつ基本的な対称性であり, 陽子 (p) と中性子 (n) を入れ替えても核力や原子核の性質は基本的に変わらない, とされてきました。ところがいま Λ バリオンを含む原子核の質量からΛp 間と Λn 間の相互作用の違いとして荷電対称性の破れが提唱されています。直接 nn 散乱実験を行うことがほぼ不可能であるため nn の散乱長の決定は間接的なものにならざるをえません。そこで本研究では電子非弾性散乱(e, e')の仮想光子 γ^* を用いた γ^*d→π⁺nn 反応で nn 散乱長を精密に測定します。実験は, 超高分解能磁気スペクトロメータを 3 つ保有し, 電子, π⁺ の散乱角, 運動量を高分解能で測定できるドイツ MAMI 施設で行う予定です。電磁相互作用の効果を補正した pp の散乱長と比較することで荷電対称性の破れを定量的に議論し, 破れの起源を解明することを目指します。

荷電対称性は強い相互作用がもつ基本的な対称性であり, 陽子 (p) と中性子 (n) を入れ替えても核力や原子核の性質は基本的に変わらない, とされてきました。素過程で考えると u クォークとd クォークの入れ替えに対する対称性であり, その破れの度合いは高々 u クォークと d クォークの質量差, 電磁相互作用の効果の違い程度と考えられます。ところが最近になって Λ バリオンを含む原子核の質量から Λp と Λn 間の相互作用の違いとして荷電対称性の大きな破れが提唱されています [1] 。核子 (N) どうしの散乱の場合はどうでしょうか? アイソスピン 1 が保証される pp 散乱と nn 散乱の散乱長aは, (電磁相互作用の効果を補正すると) a_pp = –17.3±0.4 fm, a_nn = –18.6±0.4 fm であることが知られており [2] , クォークの質量差が与える影響は高々 0.3 fm なので [3] 説明できない有意な差異と考えられます。 a_pp の決定では, 統計誤差が極めて小さく, 電磁相互作用の効果を補正する時の不定性が大きくなっています。一方, a_nn の決定では電磁相互作用が第一義的には影響しないので, 実験での統計誤差が大きくなっています。

一見, それなりに精度良く決まっているように見える a_nn ですが, 終状態での nn 散乱を通しての決定であり,

  π^–d → nnγ 反応
  nd → nnp 反応

の二種類の反応に大別されます。π^–d → nnγ 反応については生成振幅の不定性が大きく, nd → nnp 反応については必ず三体以上が関与し, 終状態における np 散乱などの効果を必ずしも除去し切れていない, という実験的な問題が存在しています。

nn → nn 散乱の効果を引き出すためには, nn 間の相対運動量をいかに小さくするか, それ以外の終状態相互作用の効果をいかに抑えるかが重要となります。

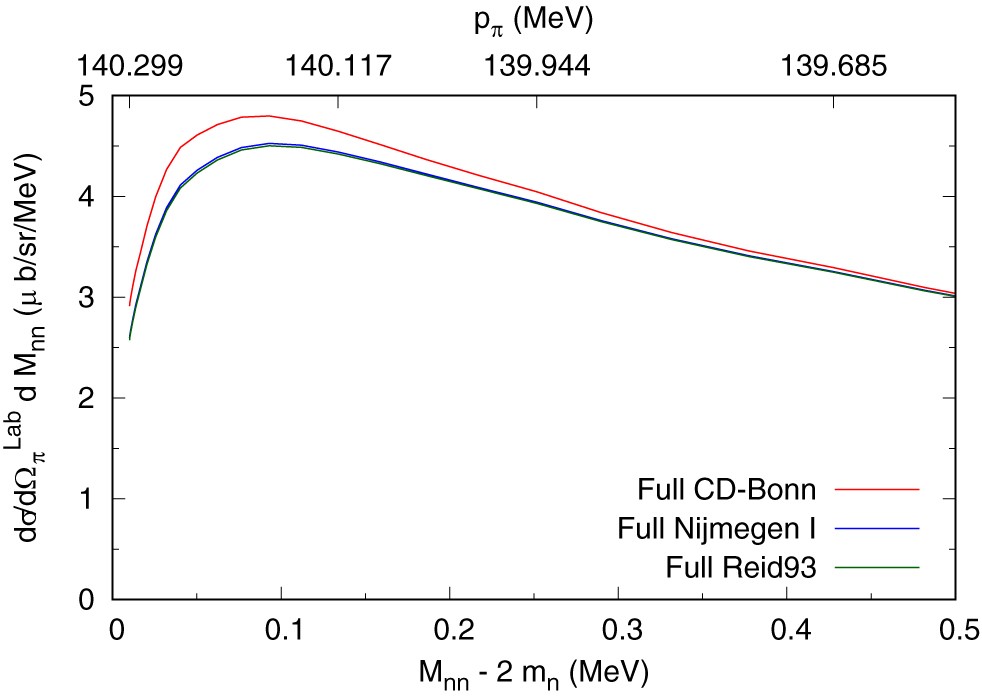
200 MeV の光子ビームを d に入射し, π⁺を 0° で検出した時の γ^*d → π⁺nn 反応の nn 不変質量 (π⁺ の運動量) に対する微分断面積 d³σ/dM_nndΩ (理論計算による予測)。CD-Bonn ポテンシャルでの nn 散乱長は –18.9 fm, Nijmegen I, Reid93 ポテンシャルでの散乱長は –17.3 fmです。CD-Bonn ポテンシャルだけが pp 散乱と nn 散乱で別々の散乱長となっています。

本研究では, (e, e') の仮想光子 γ^* を用いた γ^*d → π⁺nn 反応による nn 散乱長の決定を行います。200 MeV 程度のγ^*に対して散乱角 0° に放出された π⁺ メソンの運動量分布が, まさに散乱長を反映した nn 間の相対運動量分布を与えます。この反応の生成振幅はチャンネル結合のメソン・バリオン散乱を記述する理論モデルでよく把握されており [4], π⁺n 間の相対運動量が大きい領域を対象とすることで nn 散乱の寄与を最大化できます。図 1 に 200 MeV の光子ビームを重陽子標的 d に入射し, π⁺ を 0° で検出した時の γ^*d → π⁺nn 反応の nn 不変質量 (あるいは π⁺ の運動量) に対する理論計算で予測した微分断面積 d³σ/dM_nndΩ を示します。3 つの核力ポテンシャルを使っていますが, CD-Bonn ポテンシャルだけ pp 散乱と nn 散乱で別々の散乱長となっています。使用した核力ポテンシャルの違いが微分断面積の違いを与えています。この微分断面積を精度良くかつ正確に測定することで正しい散乱長がわかります。本当に pp 散乱と nn 散乱に対する散乱長がちがうのか, またどのくらい違うのかが議論できるようになります。

実験はドイツ Mainz MAMI 施設の電子ビームを使って行います。電子非弾性散乱 (e, e') 反応で200 MeV 程度の γ^* を生成し, γ^* の運動量方向に散乱される γ^*d → π⁺nn 反応の π⁺ の運動量分布を測定します。図1 に見られるように 139.9–140.3 MeV/c といった非常に狭い領域での角度微分断面積を精度良く決定することではじめて nn の散乱長が決定できます。一般に, 光子ビームのエネルギー標識化の分解能はそれほど高くありません。そのため標識化エネルギーの分解能の影響で π⁺ 運動量分布はぼやけてしまいます。(e, e') 反応の仮想光子を使うことで, 入射光子のエネルギー分解能を格段に向上させることができます。また MAMI 施設での電子ビームのエネルギー分解能は 10^–6 のオーダー, スペクトロメータの分析運動量分解能は 10^–4 のオーダーなので, 200 MeV の γ^* で放出される π⁺ の運動量に対して悪くても 0.1 MeV/c の運動量分解能が期待できます。

正確に求められた a_nn は電磁相互作用の効果を補正した a_pp と比較し, n と p の質量差, ρ⁰ メソンと ω メソンの混合などのその他の荷電対称性の破れに関する測定量と共に検証することで, 破れの起源の解明が期待できます。さらにこれまで原子核の構造や反応計算に使われてきた様々な核力モデルについても多大な影響を与えると考えられます。

メンバー

関連資料

• [1] A. Esser et al., Phys. Rev. Lett. 114, 232501 (2015); T. O. Yamamoto et al., Phys. Rev. Lett. 115, 222501 (2015).
• [2] E.S. Konobeevski, S. V. Zuyev, V. I. Kukulin, V. N. Pomerantsev, arXiv:1703.00519 (2017).
• [3] G.A. Miller, B.M.K. Nefkens, I. Šlaus, Phys. Rep. 194, 1 (1990).
• [4] H. Kamano, S. X. Nakamura, T. -S. H. Lee, T. Sato, Phys. Rev. C 88, 035209 (2013); ibid. 94, 015201 (2016).
• [5] S. X. Nakamura, H. Kamano, T. Ishikawa, Phys. Rev. C 96, 042201 (R) (2017).
• [6] T. Ishikawa et al., Acta Phys. Polon. B 48, 1801 (2017).